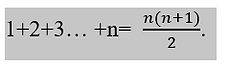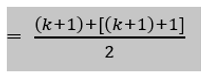La inducción matemática es un método de demostración que se utiliza cuando se trata de establecer la veracidad de una lista infinita de proposiciones.

Si con cada entero positivo n está asociado un enunciado Pn, entonces todos los enunciados Pn son verdaderos, siempre que se satisfagan las siguientes dos condiciones.

(1) P1es verdadero.

(2) Siempre que k sea un entero positivo tal que Pk sea verdadero, entonces Pk+1 también es verdadero.

Para ayudarnos a entender este principio, consideramos una sucesión infinita de enunciados marcados como.

​

 

​

 

 

 

que satisfacen las condiciones (1) y (2). Por (1), el enunciado P1es verdadero.Como la condición (2) se cumple, siempre que el enunciado Pk sea verdadero el siguiente enunciado Pk+1 también es verdadero. En consecuencia, como P1es verdadero, P2 es también verdadero, por (2). No obstante, si P2 es verda-dero, entonces, por (2), vemos que el siguiente enunciado P3 es verdadero. Una vez más, si P3 es verdadero, entonces, por (2), P4 también es verdadero. Si continuamos de este modo, podemos decir que si n es cualquier entero particular,entonces Pn es verdadero, porque podemos usar la condición (2) un paso a la vez, finalmente llegando a Pn. Aun cuando este tipo de razonamiento no demuestra realmente el principio de inducción matemática, lo hace plausible. El principio se demuestra en álgebra avanzada usando postulados para los enteros positivos.Cuando apliquemos el principio de inducción matemática, siempre seguimos dos pasos.

1 Demostrar que P1es verdadero.

2 Suponer que Pk es verdadero y luego demostrar que Pk+1es verdadero.

Es frecuente que el paso 2 cause confusión. Observe que no demostramos que Pk es verdadero (excepto para k= 1). En cambio, demostramos que si Pk es verdadero, entonces el enunciado Pk+1 también es verdadero. Nos referimos a la suposición de que Pk es verdadero como la hipótesis de inducción.

EJEMPLO 1

Use inducción matemática para demostrar que para todo entero positivo n, la suma de los primeros n enteros positivos es

​

​

​

​

 

​

 

 

 

 

SOLUCIÓN Si n es cualquier entero positivo, denotemos con Pn el enunciado.

​

​

​

 

​

 

 

 

Los siguientes son algunos casos especiales de Pn.

Si n=1, entonces P1 es

​

​

 

​

 

 

 

Si n= 2, entonces P2 es

​

​

​

​

 

​

 

 

 

Si n =3, entonces P3 es

​

​

​

 

​

​

​

 

Aun cuando es instructivo comprobar la validez de Pn para diversos valores de n como lo hemos hecho, no es necesario hacerlo. Sólo necesitamos aplicar el proceso de dos pasos indicado antes de este ejemplo. Entonces, procedemos como sigue:

Paso 1 Si sustituimos n =1 en Pn, entonces el lado izquierdo contiene sólo el número 1 y el lado derecho

 

 

 

 

 

 

 

 

 

 

es que también es igual a 1. Por tanto, P1 es verdadero.

Paso 2 Suponga que Pk es verdadero. Así, la hipótesis de inducción es

​

 

 

 

 

 

 

Nuestra meta es demostrar que Pk+1es verdadero, es decir, que

​

 

 

 

 

 

 

 

Podemos demostrar que la última fórmula es verdadera al escribir el lado

izquierdo y usar la hipótesis de inducción como sigue:

                                          

 

                                            agrupar los primeros k términos

 

 

 

 

 

                                               

 

 

                                                     hipótesis de inducción

​

​

​

 

​

                                                 

 

 

                                                          sumar términos

​

​

​

​

​

 

                                                           factorizar k+1

​

​

​

 

 

                                             

 

 

                                                       cambiar forma de k+ 2

​

​

​

​

​

​

 

 

 

Esto demuestra que Pk+1 es verdadero y por lo tanto la demostración por inducción matemática está completa.

​

VIDEO EXPLICATIVO.

​

​

​

​

​

​

​

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Bibliografía:

Swokowski, E. W; & Cole, J. A,(2009). Álgebra y Trigonometría con Geometría Analítica, Décimo Segunda edición,México: Cengage Learning Editores, S.A. de C.V.

​

Comentarios

​

​

​

​

​